Donnerstag, 5. August 2004
armkugelkonstruktion für nichtmathematiker
stricker, 14:55h
da der armausschnitt bei meinem ringelshirt eine kurve mehr hat als (bei stricksachen) üblich, habe ich mich entschieden mit angelas pythagoräischer armkugel zu konkurrieren und (auch weil mein taschenrechner nicht radizieren mag) empirischer (ich wiederhole mich) an die sache heranzugehen. ich habe also einfach die länge der rundung des armauschnitts ausgemessen, gut zwei cm dazugegeben und diese länge (im maßstab 1:2) auf einer kordel markiert. dank des Actual Size Graph Papers kann man nun ganz einfach die kordel in form legen:
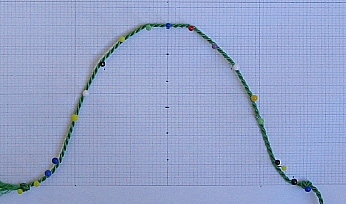
einfach die endpunkte und den scheitelpunkt (mindestens 2 cm niedriger als die höhe des armauschnitts: die länge der kordel setzt von allein die grenze, wenn man "nach gefühl" die form der kurve legt) feststecken, der rest formt sich dann fast von allein zur bekannten kurve. dann wird die kurvenlinie abgezeichnet und entsprechend des rasters (unter berücksichtigung einer gewissen regelmäßigkeit) "entrundet". jetzt kann man problemlos die abnahmen ablesen. ganz einfach ....

einfach die endpunkte und den scheitelpunkt (mindestens 2 cm niedriger als die höhe des armauschnitts: die länge der kordel setzt von allein die grenze, wenn man "nach gefühl" die form der kurve legt) feststecken, der rest formt sich dann fast von allein zur bekannten kurve. dann wird die kurvenlinie abgezeichnet und entsprechend des rasters (unter berücksichtigung einer gewissen regelmäßigkeit) "entrundet". jetzt kann man problemlos die abnahmen ablesen. ganz einfach ....
... comment
nispi,
Donnerstag, 5. August 2004, 16:13
Bin zwar Mathematikerin
finde diese Idee aber trotzdem klasse. Sogar so gut, dass ich das unter meinem Technik-Ordner speichern werde!
Nina
Nina
... link
ingi,
Donnerstag, 5. August 2004, 17:17
Klasse!!!!
Sollte ich Anleitungsheft-Junkie je in der Situation sein, eine Armkugel berechnen zu müssen, dann werde ich auf Dein System zurück greifen.
Liebe Grüße,
Inga
Liebe Grüße,
Inga
... link
... comment
angela,
Donnerstag, 5. August 2004, 23:29
Das ist wirklich besser!
Lieber Jörg,
mein Pythagoras liefert ja sowieso nur die Höhe der Armkugel. Die Krümmung selbst ist dann wieder Intuitions-Sache und man "schwimmt" dabei im Unklaren, bis man jedesmal wieder merkt, dass es klappt... :-)
Außerdem schreckt das Wurzelziehen ja überhaupt jeden ab, mein Beitrag scheint die Armkugelosen eigentlich noch zu bestärken ;-)
Liebe Grüße
Angela
(die ihre Fäden auch so vernäht...)
mein Pythagoras liefert ja sowieso nur die Höhe der Armkugel. Die Krümmung selbst ist dann wieder Intuitions-Sache und man "schwimmt" dabei im Unklaren, bis man jedesmal wieder merkt, dass es klappt... :-)
Außerdem schreckt das Wurzelziehen ja überhaupt jeden ab, mein Beitrag scheint die Armkugelosen eigentlich noch zu bestärken ;-)
Liebe Grüße
Angela
(die ihre Fäden auch so vernäht...)
... link
stricker,
Freitag, 6. August 2004, 12:48
ach, du hast wieder recht
liebe angela. ich meine damit natürlich nicht, dass "meine" methode besser ist, sondern dass sich beide ergänzen: also wird die höhe pythagoräisch berechnet, die rundung dann empirisch. nach gefühl runden reicht natürlich ... aber so ist es wirklich idiotensicher (und geht etwas schneller).
dieses millimeterpapier nach maß ist aber schon eine tolle idee. ich dachte da vor allem an intarsienmuster (bei einstrickmustern reicht ja quadratisches, nicht?). da hab ich auch schon wieder eine idee ...
übrigens: wer nicht wurzeln ziehen will kann das ganze eigentlich doch einfach auch aufzeichnen und ausmessen...
liebe grüße,
jörg
dieses millimeterpapier nach maß ist aber schon eine tolle idee. ich dachte da vor allem an intarsienmuster (bei einstrickmustern reicht ja quadratisches, nicht?). da hab ich auch schon wieder eine idee ...
übrigens: wer nicht wurzeln ziehen will kann das ganze eigentlich doch einfach auch aufzeichnen und ausmessen...
liebe grüße,
jörg
... link
kelef,
Sonntag, 8. August 2004, 01:11
nochmal die uroma von meiner oma
ohne mathematik, sondern mit hausverstand:
ärmel so weit stricken, bis die richtige länge - festgestellt durch einklemmen unter der achsel und dann muss er bis zur richtigen stelle am handgelenk reichen, oder umgekehrt - erreicht ist.
dann bei aufeinanderfolgenden reihen erst drei, dann zwei, dann immer eine masche am anfang abnehmen: drei und zwei abketteln, dann immer zusammenstricken. dies so lange, bis - wieder bei unter der achsel eingeklemmtem ärmel, bei für fremdpersonen lt. cm - die richtige länge erreicht ist. diese liegt so bei ca. 3 cm unter der achselnaht. dann nach gefühl leicht steigernd auf fünf- bis sechsmal symmetrisch abketteln, bis zum nullpunkt. beispiel: 2xdrei - 2xfünf - 2xsieben - 2xneun. bei ein wenig erfahrung resp. augenmass ganz einfach, und passt immer und jedem, seit generationen.
ärmel so weit stricken, bis die richtige länge - festgestellt durch einklemmen unter der achsel und dann muss er bis zur richtigen stelle am handgelenk reichen, oder umgekehrt - erreicht ist.
dann bei aufeinanderfolgenden reihen erst drei, dann zwei, dann immer eine masche am anfang abnehmen: drei und zwei abketteln, dann immer zusammenstricken. dies so lange, bis - wieder bei unter der achsel eingeklemmtem ärmel, bei für fremdpersonen lt. cm - die richtige länge erreicht ist. diese liegt so bei ca. 3 cm unter der achselnaht. dann nach gefühl leicht steigernd auf fünf- bis sechsmal symmetrisch abketteln, bis zum nullpunkt. beispiel: 2xdrei - 2xfünf - 2xsieben - 2xneun. bei ein wenig erfahrung resp. augenmass ganz einfach, und passt immer und jedem, seit generationen.
... link
stricker,
Sonntag, 8. August 2004, 01:40
pst! nicht verraten ...
das klappt natürlich wunderbar mit deiner hausmethode, da bin ich mir sicher: etwas anderes kommt auch bei den berechnungen - im prinzip (garnstärke!) - nicht heraus. mit einer einschränkung: sehr schmale ärmel verlangen eine sehr steile armkugel (wenn mann auf perfekten sitz und bauchfreiheit bei benutzung der oberen regalbretter besteht ...). so in meinen beispiel: ich muss im mittleren drittel jede vierte reihe eine masche abnehmen, um die nötige armkugelhöhe zu erreichen. aber auch nur wegen der streifen, die aufeinandertreffen sollen und meiner hysterie, dass der ärmel kein fältchen werfen darf.
... link
... comment